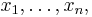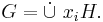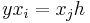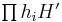Transfer (group theory)

In the mathematical field of group theory, the transfer defines, given a group G and a subgroup of finite index H, a group homomorphism from G to the abelianization H. It can be used in conjunction with the Sylow theorems to obtain certain numerical results on the existence of finite simple groups.

1 Construction
2 Example
3 Homological interpretation
4 Terminology
5 Commutator subgroup
6 See also
7 References

Construction

The construction of the map proceeds as follows:^[1] Let [G:H] = n and select coset representatives, say

$x_1, \dots, x_n,\,$

for H in G, so G can be written

$G = \dot{\cup}\ x_i H.$

Given y in G, each yx_i is in some coset x_jH and so

$yx_i = x_jh$

for some index j and some element h of H, Then in general

$yx_i = x_{iA}h_i$

where A=A(y) is some mapping of {1,2,…,n} to itself and each h_i=h_i(y) is an element of H.

The value of the transfer for y is defined to be the product in H/H′

$\textstyle \prod h_i H'$

where H′ is the commutator subgroup of H. Note that the order of the factors is irrelevant since H/H′ is abelian.

It's straightforward to show that, though the individual h_i depend on the choice of coset representatives, the value of the transfer does not. It's also straightforward to show that and that the mapping defined this way a homomorphism.

Example

A simple case is that seen in the Gauss lemma on quadratic residues, which in effect computes the transfer for the multiplicative group of non-zero residue classes modulo a prime number p, with respect to the subgroup {1, −1}. One advantage of looking at it that way is the ease with which the correct generalisation can be found, for example for cubic residues in the case that p − 1 is divisible by three.

Homological interpretation

This homomorphism may be set in the context of group cohomology (strictly, group homology), providing a more abstract definition. The transfer is also seen in algebraic topology, when it is defined between classifying spaces of groups.

Terminology

The name transfer translates the German Verlagerung, which was coined by Helmut Hasse.

Commutator subgroup

If H is the commutator subgroup G′ of G, then the corresponding transfer map is trivial. In other words, the map sends G to 0 in the abelianization of G′. This is important in proving the principal ideal theorem in class field theory. See the Emil Artin-John Tate Class Field Theory notes.

References

^ Following Scott 3.5

Scott, W.R. (1987). Group Theory. Dover. p. 60 ff.. ISBN 0486653773.